以下文字摘錄自:四分位数 - 维基百科,自由的百科全书
四分位數 (英語:Quartile)是統計學中分位數的一種,即把所有數值由小到大置換並分成四等份,處於三個分割點位置的數值就是四分位數。
一個算法如下(可以兼用TI-83計算器):
- 利用中位數使數據分成兩列(不要把中位數放入已分好的數列)。
- 第一四分位數為第一組數列的中位數;第三四分位數為第二組數列的中位數。
例1
數據總量:6,47,49,15,42,41,7,39,43,40,36
由小到大置換的結果:6,7,15,36,39,40,41,42,43,47,49
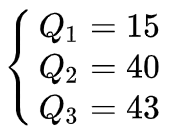
例2
數據總量:7,15,36,39,40,41
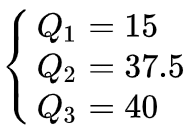
例3
數據總量:1,2,3,4
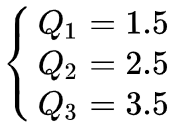
箱形圖
上圖示中箱形圖(有四分位數及四分位距)和機率密度函數 為描述一個常規總量的分布情況
在LabVIEW計算中位數
參考:https://forum.stdb.org/t/topic/31158 ,使用Median VI就可以計算一個1D Array的中位數。
在LabVIEW計算第1四分位數(Q1)
LabVIEW中沒有直接計算第1四分位數(Q1)的函數。但是你可以依序以下方法找出第1四分位數(Q1):
- 先用Median VI就可以計算一個X Array 的中位數
- 選出數值小於中位數的所有數值,並設為X’ Array
- 使用Median VI計算X’ Array的中位數,即為第1四分位數(Q1)
在LabVIEW計算第3四分位數(Q3)
LabVIEW中沒有直接計算第3四分位數(Q3)的函數。同理,你可以依序以下方法找出第3四分位數(Q3):
- 先用Median VI就可以計算一個X Array 的中位數
- 選出數值大於中位數的所有數值,並設為X’’ Array
- 使用Median VI計算X’’ Array的中位數,即為第3四分位數(Q3)
四分位數的功用
請參考上面的箱型圖:
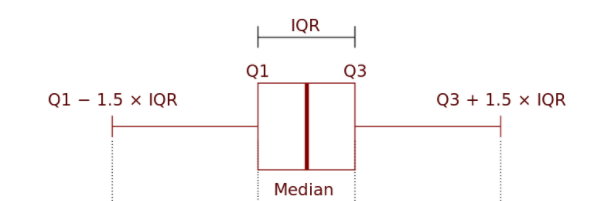
四分位距 IQR (interquartile range)
四分位距 (英語:interquartile range, IQR)。是描述統計學中的一種方法,以確定第三個四分位數和第一個四分位數的差值(即Q1, Q3的差距)[1]。與變異數、標準差一樣,表示統計資料中各變量分散情形,但四分差更多為一種穩健統計(robust statistic)。
四分位差 (Quartile Deviation, QD)
是Q1, Q3差距的一半,即為:
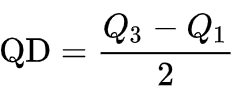
內限
下內限:Q1 - 1.5*IQR
上內限:Q3 + 1.5*IQR
外限
下內限:Q1 - 3*IQR
上內限:Q3 + 3*IQR
處於內限以外的數據即為異常值;在內限與外限之間的異常值為溫和的異常值(mild outliers),在外限以外的為極端的異常值(extreme outliers)。
去除離群值
在內限外的數值,在統計上稱為溫和的異常值。統計上會把溫和的異常值去除,也就是去除離群值。